the equatorial coordinate system back to teaching back to the course first page of this section previous page next page last page of this section start of next section help on navigating these pages



Because the altitude and azimuth of a star are constantly changing, it is not possible to use the horizontal coordinate system in a catalogue of positions. A more convenient coordinate system for cataloguing purposes is one based on the celestial equator and the celestial poles and defined in a similar manner to latitude and longitude on the surface of the Earth. In this system, known as the equatorial coordinate system, the analogue of latitude is the declination, . The declination of a star is its angular distance in degrees measured from the celestial equator along the meridian through the star. It is measured north and south of the celestial equator and ranges from 0° at the celestial equator to 90° at the celestial poles, being taken to be positive when north of the celestial equator and negative when south. In Figure 15, the declination of the star X is given by the angle between Y and X.

The analogue of longitude in the equatorial system is the hour angle, H (you may also see the symbol HA used). Defining the observer's meridian as the arc of the great circle which passes from the north celestial pole through the zenith to the south celestial pole, the hour angle of a star is measured from the observer's meridian westwards (for both northern and southern hemisphere observers) to the meridian through the star (from 0° to 360°). Because of the rotation of the Earth, hour angle increases uniformly with time, going from 0° to 360° in 24 hours. The hour angle of a particular object is therefore a measure of the time since it crossed the observer's meridian - hence the name. For this reason it is often measured in hours, minutes and seconds of time rather than in angular measure (just like longitude). In Figure 15, the hour angle of the star X is given by the angle Z-NCP-X. Note that all stars attain their maximum altitude above the horizon when they transit (or attain upper culmination on, in the case of circumpolar stars) the observer's meridian.

The declination of a star does not change with time. The hour angle does, and hence it is not a suitable coordinate for a catalogue. This problem is overcome in a manner analogous to the way in which the Greenwich meridian has been (arbitrarily) selected as the zero point for the measurement of longitude. The zero point chosen on the celestial sphere is the first point of Aries, , and the angle between it and the intersection of the meridian through a celestial object and the celestial equator is called the right ascension (RA) of the object. Right ascension is sometimes denoted by the Greek letter and is measured from 0h to 24h along the celestial equator eastwards from the first point of Aries, that is, in the opposite direction to that in which hour angle is measured. Like the definition of hour angle, this convention holds for observers in both northern and southern hemispheres. In Figure 15, the right ascension of the star X is given by the angle -NCP-Y.

 
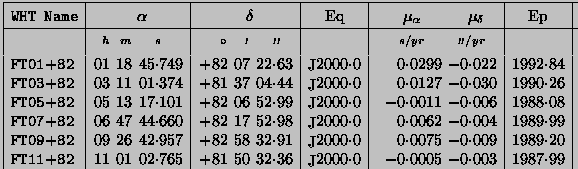
figure 15: The equatorial coordinate system.


As described previously, most modern research telescopes do not use equatorial mounts due to their higher cost and lower stability. This is at the expense of the simplicity of telescope tracking - an equatorially-mounted telescope need only move its right ascension axis in order to track the motion of the celestial sphere. Figure 16 shows an example of an equatorially-mounted telescope.

 
figure 16: An equatorially mounted telescope - the 3.9 m Anglo-Australian Telescope (AAT) in Australia.


 
In the above discussions on coordinate systems and the celestial sphere we make the assumption that the stars are fixed on the celestial sphere and never move. For accurate positional work on long timescales, this assumption does not hold - the stars do move on the celestial sphere.

The Earth's axis of rotation is not fixed in direction, but precesses slowly in space, like a spinning top, due to the gravitational attractions of the Sun and Moon on the rotating, non-spherical Earth (see page 144 of Roy and Clarke for a detailed description). Because of this, the north celestial pole traces out a small circle with a radius equal to the obliquity of the ecliptic, . This also causes the celestial equator to move, and as a result the first point of Aries is not actually a fixed reference point; it moves gradually backwards along the ecliptic, by about 50 arcseconds per year, and is in fact currently in the neighbouring constellation of Pisces. This motion is known as the precession of the equinoxes and it means that even right ascension and declination are not quite fixed coordinates and catalogues of star positions have to specify the date (e.g. 1950.0 or 2000.0) to which they refer. More precisely, the coordinate frame used for catalogue positions is defined by the position of the vernal equinox (the first point of Aries) on a particular date, so astronomers talk about positions referred to (for example) the equinox of 2000.0. Although the pole takes some 26 000 years to make one revolution, the effect of precession is much larger than the uncertainties in the positions of objects, so all positional measurements must be corrected for precession.

Precession only rotates the reference frame, and has no effect on the relative positions of stars. However, the stars are not stationary in space; they are all moving around the centre of the Galaxy, in different orbits, and the effect is that nearby stars have measurable motions relative to the Sun. The projections of these motions onto the celestial sphere are known as the stars' proper motions, usually given the symbol , and they do cause changes in the relative positions of stars. For stars with significant proper motion, it is therefore necessary to specify both the proper motion and the date of the observation (known as the epoch), as well as the catalogue position and the equinox to which it refers. If no epoch is given for a position, it is assumed that the epoch is the same as the equinox of the reference frame.

There are a number of other, generally smaller, corrections astronomers need to make to the coordinates of an astronomical object before doing accurate positional work. These include atmospheric refraction, stellar aberration and nutation, which are all described in Chapters 10 and 11 of Roy and Clarke.

You should now be able to understand a page out of a star catalogue, an example of which is shown in Table 1.

 
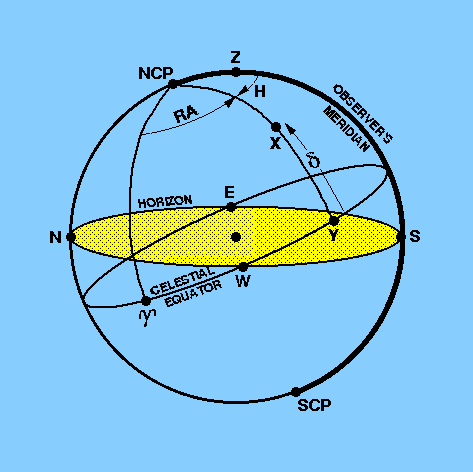
table 1: An extract from a typical star catalogue.


Using the position of the first point of Aries as the basis of the equatorial coordinate system is inappropriate for high-precision positional astronomy. This is due to the fact that the theories of motion of the Earth that define how the celestial equator and ecliptic (and hence the first point of Aries) move are imperfect. Even if these planes are defined without any reference to the motions of the Earth, there is no way to magically paint them on the celestial sphere at any particular time. Therefore, in practice, a set of fiducial objects with assigned coordinates are used to define the coordinate system. The axes of the International Celestial Reference System (ICRS), the current standard celestial reference system, are defined by the adopted positions of a specific set of extragalactic objects (mainly quasars observed in the radio), which are assumed to have no measurable proper motions. The ICRS axes are consistent to better than 0.1 arcseconds with the equinox of 2000.0 defined by the dynamics of the Earth. However, the ICRS axes are meant to be regarded as fixed directions in space that have an existence independent of the dynamics of the Earth or the particular set of objects used to define them at any given time.

©Vik Dhillon, 30th September 2009