vik dhillon: phy213 - the physics of stellar interiors

occurrence of fusion reactions

Having established that nuclear fusion rather than fission reactions are the primary source of energy generation in stars, we turn now to discuss the conditions under which fusion can occur and whether such conditions actually exist within stars.

Nuclei interact through the four forces of nature: electromagnetic, gravitational, strong nuclear and weak nuclear. In determining the conditions for nuclear fusion to occur, only the electromagnetic and strong nuclear forces are of importance. In order to fuse, two nuclei (which are always positively charged) have first to overcome the repulsive electrostatic force between them. This is a long range force which falls off with distance, r, as 1/r². Once the two nuclei are separated by less than 10^-15m (the typical size of a nucleus), the attractive (and much shorter range) strong nuclear force takes hold and draws the nuclei together. It is this strong force which holds nuclei together and which causes the nuclear reactions that occur in stars. The upper panel of figure 15 illustrates the competition between the electrostatic and strong nuclear forces.

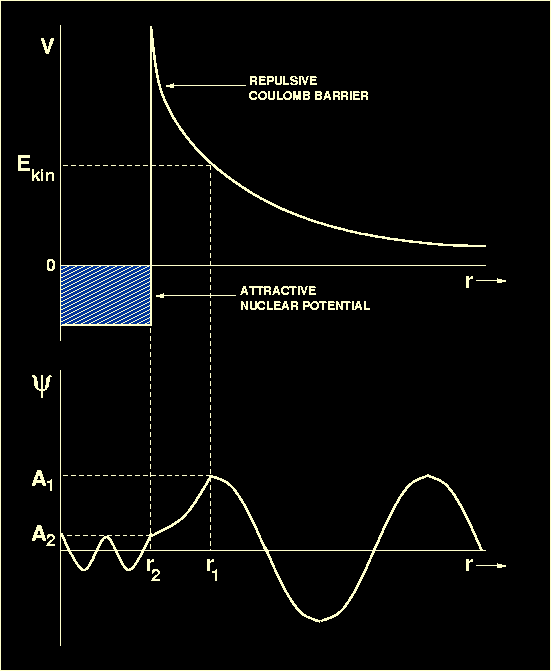
Figure 15:

Upper panel: A schematic plot of the potential energy V (i.e. the energy which one nucleus must have in order to approach another nucleus) versus separation between two nuclei. At large separations, the electrostatic repulsion dominates. For separations of r<10^-15m, the strong nuclear force takes over, allowing the two nuclei to fuse. Lower panel: A schematic plot of the wave function representing the penetration of a potential barrier by a nucleus whose kinetic energy of approach E_kin is below that of the barrier. The wave function oscillates sinusoidally in the inner and outer classically allowed regions and decays exponentially in the intervening classically forbidden region.

In order to fuse two nuclei, the upper panel of figure 15 shows that it is first necessary to surmount the potential barrier (or Coulomb barrier) set by the electrostatic repulsion. The height of the Coulomb barrier between two nuclei can be estimated using the equation

Z₁Z₂e² / 4

e₀r,

where Z₁ and Z₂ are the number of protons in each of the two nuclei. Setting r = 10^-15m, Z₁ = Z₂ = 1, the charge on the electron e = 1.60x10^-19 C and the permittivity of free space e₀ = 8.85x10^-12 C²N^-1m^-2, we obtain a potential energy of 2.3x10^-13J or 1.4 MeV for the height of the Coulomb barrier.

In classical physics, the only way a nucleus can overcome the Coulomb barrier is for it to increase its kinetic energy. We saw when discussing energy generation, that the average kinetic energy of a nucleus in an ideal gas is 3kT/2. In order to overcome the Coulomb barrier, therefore, the temperature would have to be 1.1x10¹⁰K. This is nearly four orders of magnitude higher than the minimum mean temperature of the Sun, 2x10⁶K, we derived earlier. How can these two numbers be reconciled? First, one could argue that we only estimated the minimum mean temperature of the Sun. Detailed stellar models tell us, however, that the actual central temperature of the Sun is only 1.5x10⁷K, so this still leaves a disparity of nearly three orders of magnitude. Second, 3kT/2 only gives the mean energy per nucleus, but in a perfect gas the nuclei will actually have a Maxwellian distribution of energies and hence some nuclei will have higher energies than the mean. The number of nuclei with an energy E which is higher than the average energy decreases as e^-E/kT. For an energy which is roughly 1000 times larger than the mean, the number of nuclei therefore decreases by a factor of e^-1000 or 10^-434. The total number of nuclei in the Sun is approximately given by its mass divided by the mass of a hydrogen atom, i.e. 1.99x10³⁰/1.67x10^-27 ~ 10⁵⁷. The chance of finding even one nucleus with a kinetic energy large enough to overcome the Coulomb barrier is therefore essentially zero.

It was in the face of the above arguments that Eddington made his famous remark that, if the centre of the Sun was not hot enough for the nuclear physicists, they must find a hotter place. The problem was finally solved with the advent of quantum mechanics. Heisenberg's uncertainty principle can be written in the form

h / 4

,

where

E and

t is the uncertainty in the energy of a nucleus and the time for which the particle exists in this state, respectively. If the extra energy above the classical value that an incoming nucleus requires to overcome the Coulomb barrier and the time for which it requires that energy satisfy the above equation, then there is a chance of a nuclear reaction occurring.

This effect is known as quantum mechanical tunnelling, and is illustrated in the lower panel of figure 15. The approach of a nucleus to the Coulomb barrier can be thought of in terms of a wave which is described by the Schrodinger equation. If the incoming nucleus has a kinetic energy E_kin, then according to classical theory it is unable to approach closer than r₁. For r > r₁, i.e. where E_kin > V, the wave function for the oncoming nucleus is a sine wave with amplitude A₁. For r₂ < r < r₁, E_kin < V and the wave function is an exponential function decreasing towards smaller r. For r < r₂, we find again E_kin > V and the wave function is again a sine wave but now with amplitude A₂. It is the (square of the) amplitude of the wave function that determines the probability of finding a particle at a specified position and hence the amplitude of the wave function in the region r < r₂ determines the probability for the nucleus to tunnel through the Coulomb barrier. The important point here is that amplitude of the wave function, and hence the tunnelling probability, is not zero, which means that there is a finite chance that fusion will occur even when the kinetic energy is classically too small to breach the Coulomb barrier. This does not mean, however, that the process is likely. For example, two protons, which undergo approximately 10¹⁰ collisions per second with other protons in the solar interior, survive on average for approximately 10¹⁰ years, the lifetime of the Sun. But this is sufficient to power the Sun. (Note, however, that the probability of two protons fusing depends not only on the tunnelling probability but also the probability of a ⁺ decay occurring).

It should be noted that for larger E_kin, the width of the Coulomb barrier becomes narrower (i.e. r₁-r₂ decreases), the decay of the wave function becomes less steep and the amplitude of the wave function in the region r < r₂ becomes larger (i.e. A₂/A₁ increases). Hence the tunnelling probability increases if the kinetic energy of the incoming nucleus increases. According to the Maxwellian distribution, however, the number of particles decreases as their kinetic energy increases. Therefore, fusion mostly occurs in an energy window defined by the so-called Gamow peak, as shown in figure 16.

Figure 16:

The Gamow peak (solid curve) is the product of the Maxwellian distribution and the tunnelling probability. Most fusion reactions take place between particles with relative energies lying within the Gamow peak. The area under the Gamow peak determines the reaction rate.

It should also be noted that the higher the electric charges of the interacting nuclei, the greater the repulsive force between them and the higher the kinetic energy (and hence temperature) must be before nuclear reactions can occur. The highly charged nuclei are also the more massive nuclei and this means that nuclear reactions between light elements occur at lower temperatures than nuclear reactions between heavy elements.