An astronomical spectrograph splits, or disperses, the light from a source into its component wavelengths. Some means of dispersing the light is therefore required. This function used to be performed by a prism, which exploits the fact that light of different wavelengths are refracted by different amounts, with blue light being refracted more than red light, as shown in figure 86. Prism spectrographs are only rarely found in astronomical spectrographs nowadays. There are a number of reasons for this, including: the dispersion is non-linear, with light in the blue part of the spectrum being dispersed more than the red, making it more difficult to analyse; the dispersion is not very high, and the only way of significantly increasing it is to use two or more prisms in tandem, which starts to become inefficient due to the loss of light at each air-glass surface and absorption within the glass itself.

figure 86:

A photograph showing how white light entering a prism from the left is dispersed into a spectrum on exiting at the right. Note how the blue light is refracted by the greatest angle and also dispersed the most.

The almost universal choice for the dispersing element in modern astronomical spectrographs is the diffraction grating. A diffraction grating consists of a large number of fine, equidistant, parallel lines ruled onto a transparent glass plate so that light can pass between the lines, but not through them. Strictly speaking, this would be a transmission grating; a reflection grating would have the lines ruled onto a reflective glass plate so that only the light falling between the lines is reflected. An example of each is shown in figure 87. Gratings with up to 2400 lines per mm are available, produced either with a diamond tool or photolithographic (holographic) etching.

figure 87:

Left: photograph of a transmission grating for the amateur astronomy market with 100 grooves per mm. Centre: photograph of a reflection grating mounted in a professional spectrograph. Right: a microscopic view of the grooves in a typical diffraction grating.

     

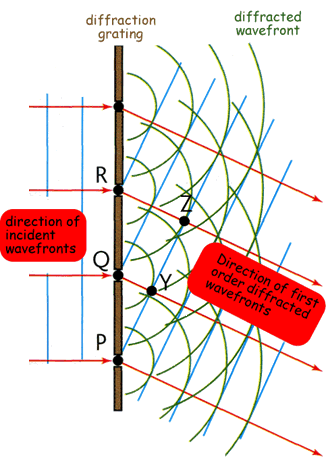
Light incident upon a grating will be diffracted by the lines, producing a series of secondary wavelets emanating from the gaps between the lines, as shown in the left-hand panel of figure 88. As each diffracted wavefront emerges from a gap, it reinforces wavefronts from each of the other gaps, i.e. there is constructive interference, but only at certain angles. For example, in the left-hand panel of figure 88, the monochromatic wavefront emerging at P reinforces the wavefront emitted from Q one cycle earlier, which reinforces the wavefront emitted from R one cycle earlier, etc. The effect is to form a new wavefront PYZ which travels in a certain direction and contributes to the first-order diffracted beam. A similar diagram could be drawn for a second-order diffracted beam, but in this case the wave emerging at P reinforces the wavefront emitted from Q two cycles earlier, etc. The end result is shown in the centre-left panel of figure 88, which shows that multiple orders emerge from a diffraction grating.

figure 88:

Schematic showing how parallel, monochromatic wavefronts are diffracted by the gaps in the grating, forming secondary wavefronts which constructively interfere (left), transmitting light in certain directions only (centre-left). Constructive interference only occurs when the path difference between the wavefronts is equal to a whole number of wavelengths (centre right - for incident waves perpendicular to the grating; right - for arbitrary angle of incidence).

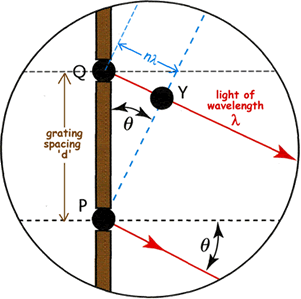
The condition for constructive interference can be derived by inspecting the centre-right panel of figure 88. The wavefront emerging from slit P reinforces a wavefront emitted n cycles earlier by the adjacent slit Q. This earlier wavefront therefore must have travelled a distance of n wavelengths from the slit. Therefore the perpendicular distance QY from the slit to the wavefront is equal to nλ, where λ is the wavelength of the light. Since the angle of diffraction of the beam, , is equal to the angle between the wavefront and the plane of the slits, it follows that sin = QY/QP, where QP is the grating spacing (i.e. the centre-to-centre distance d between adjacent slits). Substituting d for QP and nλ for QY and rearranging gives the grating equation:

n λ = d sin .

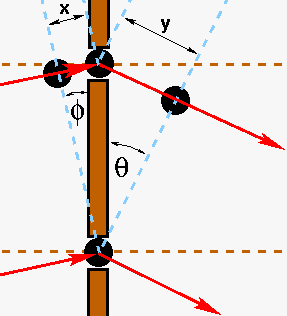
In deriving the above form of the grating equation, we assumed an incident beam perpendicular to the grating. If, instead, the incident beam makes an angle with respect to the grating, then the right-hand panel of figure 88 shows that the total path difference becomes x + y = nλ. Given this, we arrive at the more generalized form of the grating equation:

n λ = d (sin + sin ).

The discussion above has considered only a monochromatic incident wavefront. If more than one wavelength is present, each wavelength will be diffracted through different sets of angles as defined by the grating equation. The diffraction grating will thus disperse the light incident upon it into its component wavelengths, as shown in figure 89. It can be seen that the zeroth order is undispersed, which follows from the grating equation - when n = 0, then = 0 and hence light of all wavelengths is undeviated. The first orders (n = ±1) fall either side of the zeroth order, with the blue light deviated the least and red the most, opposite to that observed with a prism (figure 86). This follows from the grating equation - for a fixed n and d, must increase as λ increases. Outside the first order can be seen the second (n = ±2) and third (n = ±3) orders, which appear successively wider and fainter. As we shall see, the higher dispersion in higher orders is exploited in high-resolution spectrographs, in conjunction with blazed gratings to overcome the efficiency loss.

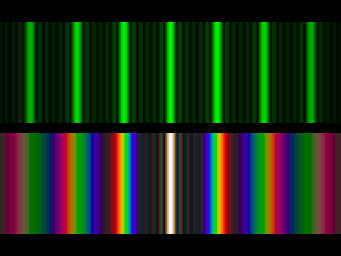
figure 89:

Photograph showing the diffraction pattern produced by a monochromatic light source (top) and a white light source (bottom) incident on a diffraction grating. The central bright line is the zeroth order, with orders ±1, ±2 and ±3 shown either side of this. The fainter lines between the bright lines are due to the diffraction pattern produced by the finite width of the grooves in the grating.