Astronomers studying the Universe from the surface of the Earth have to peer through the atmosphere. This has a number of undesirable consequences:

• Sky background: Dust and molecules in the atmosphere scatter light from the Moon and the surface of the Earth (e.g. street lamps), making the entire sky appear to glow. The molecules in the atmosphere also emit light. The sky therefore acts as a noisy background to the light received from astronomical objects, making the detection of faint targets particularly difficult.
  
  
• Atmospheric extinction: Dust and molecules in the atmosphere scatter and absorb the light from astronomical objects, dimming the images obtained by astronomical telescopes. The amount of dimming depends on the angle of the object above the horizon and the local conditions in the atmosphere at the time of observation. This type of extinction is prefixed with the word atmospheric in order to distinguish it from interstellar extinction.
  
  
• Transparency variations: Related to atmospheric extinction, clouds (i.e. water droplets) can absorb and scatter the light from astronomical objects. The amount of absorption tends to be much more variable than that due to extinction, as the clouds are blown across the field of view of the telescope by the wind. The resulting variations in the amount of light received from an astronomical object range from partial attenuation due to thin cloud, to complete obscuration by thick cloud.
  
  
• Seeing: Completely unrelated to the above effects, turbulence in the atmosphere degrades the resolution of the image recorded by a telescope. We shall look at the causes and effects of seeing in more detail below. The turbulence also causes a variation in the brightness of an image recorded by a telescope, a phenomenon known as scintillation (or, less formally, twinkling), but this will not be considered further here.

  It is very important not to confuse seeing and transparency. The two effects are largely unrelated: in poorer seeing, the image of a star will be more blurred, but its brightness will remain approximately constant; in poor transparency, the light from a star will be dimmed but its blurring will be largely unaffected.

Turbulence in the atmosphere occurs on all scales and results in adjacent pockets of air with slight temperature differences between them. Since the temperature of air affects its density, which in turn affects its refractive index, some rays of light from an astronomical source are bent by more than others. In terms of wavefronts, the plane wavefront from a star is corrugated by the atmosphere, as some parts of it are retarded in phase by more than others. This is shown schematically in figure 42.

figure 42:

Schematic showing the effect of atmospheric turbulence on image formation in both a small and large-aperture telescope.

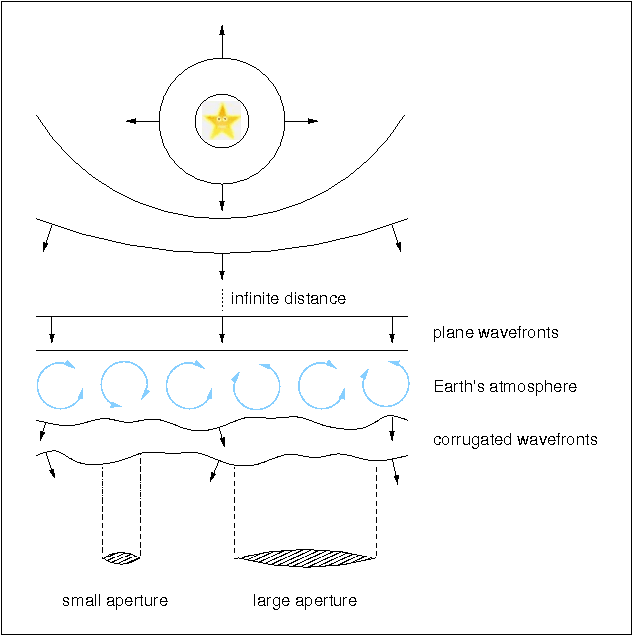
It can be seen from figure 42 that the image of a star will look very different through telescopes of different aperture. Small-aperture telescopes will collect portions of the wavefronts which do not have many corrugations. We have already seen that straight portions of a wavefront produce diffraction-limited images, hence the instantaneous image of a star in a small-aperture telescope (of order 10 cm, the typical size of the straight portion of a wavefront) will generally appear diffraction limited, as shown in the left-hand panel of figure 43, but the image will dance around on timescales of a fraction of a second. This is because the straight portions of successive wavefronts have different slopes with respect to the telescope aperture and hence will be focused onto different points in the focal plane. The effect of exposing for many seconds or minutes then is to average out this image motion into a single blurred image of the star, similar to that shown in the right-hand panel of figure 43, This is known as the seeing disc.

Large aperture telescopes (>> 10 cm) collect wavefronts with many corrugations. Each of the straight portions of the wavefront are simultaneously brought to a sharp focus, but at positions in the focal plane dependent on their tilts. Hence the instantaneous image appears as small bright spots, or speckles, superimposed on a faint, blurred disc, as shown in the central panel of figure 43. The effect of accumulating many such images over the course of seconds or minutes is to average them out into a seeing disc similar to that seen through a small telescope, as shown in the right-hand panel of figure 43. Note that, since each speckle in the instantaneous image is made up of all of the straight portions of the wavefront with the same tilt, and the maximum separation of these straight portions is given by the diameter of the aperture, the speckles will have a typical size given by the diffraction limit of the aperture. In other words, each speckle is a diffraction-limited image produced by the large-aperture telescope, explaining why the speckles appear so small in the central panel of figure 43.

figure 43:

Left: Example of a short-exposure (of order milliseconds) image of a point source through a ~10 cm ground-based telescope. The fact that the first diffraction ring can just be seen surrounding the Airy disc implies that the instantaneous resolution is close to the diffraction limit, but significant image motion would cause blurring in a longer exposure, similar to that shown in the right-hand panel. Centre: Short-exposure image of a point source through a ~1 m ground-based telescope. The image is broken up into bright, dancing speckles, which are smeared-out in the longer-exposure image shown in the right-hand panel.

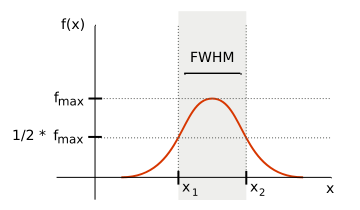
A measurement of the full-width at half-maximum (FWHM) of the seeing disc gives a numerical value for the seeing, as shown in figure 44. The value x₂-x₁ is typically measured in pixels from an astronomical image and then converted to arcseconds using the plate scale of the telescope. Seeing as low as 0.1 arcseconds has been recorded on the Earth's surface in Antarctica. The typical seeing at premier astronomical observatories, such as those found in Hawaii, Chile or the Canaries, is between 0.5 and 1.0 arcseconds. The best we've recorded from the roof of the Physics building in Sheffield is about 2 arcseconds! Given that the diffraction limit of a 10 cm telescope is approximately 1 arcsecond, it can be seen that in all but the smallest-aperture telescopes, the resolving power of a ground-based telescope is limited not by diffraction but by the seeing.

figure 44:

Schematic showing the seeing profile of a star and how the FWHM is measured.

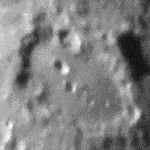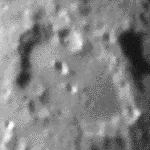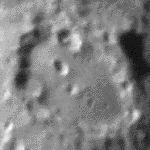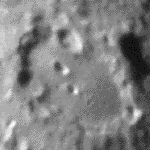
A good way to appreciate the disastrous consequences of astronomical seeing on image quality is to look at movies of both point sources and extended sources, such as those shown in figure 45. To minimise the effects of the seeing shown in the movies below, astronomers continually seek new places to site their telescopes, a topic we shall turn to next.

figure 45:

Examples of the effects of astronomical seeing on image quality. Left: Images of a star obtained on a large amateur telescope using a webcam with 0.01 s exposures. Each image is separated in time by about 1 second. Centre: A movie of a star observed with the Russian 6 m telescope, showing the speckle pattern. Note the image scale. Right: An amateur astronomer's movie of the lunar crater Clavius taken in bad seeing conditions.

  

As well as blurring the images of stars, atmospheric turbulence also induces intensity variations, known as scintillation. A detailed description of this phenomenon can be found in the paper by Osborn et a. (2016), and references therein. It should be noted that scintillation is actually an interference phenomenon, caused by diffraction of formerly plane-wave light distorted by atmospheric turbulence (see Little 1951, Chandrasekhar 1952 and this web page by Kuehne).