The role of the eyepiece and the eye

It is rarely possible to look through modern research telescopes with the eye. This is because observing time on them is so precious and because the eye is such a poor detector compared to the electronic equivalents. On the other hand, amateur telescopes are often used visually, in which case an eyepiece is required, as shown in figure 27.

figure 27:

Schematic of a refracting telescope, illustrating the role of the eyepiece and the eye. The same concepts would apply if considering a reflecting telescope.

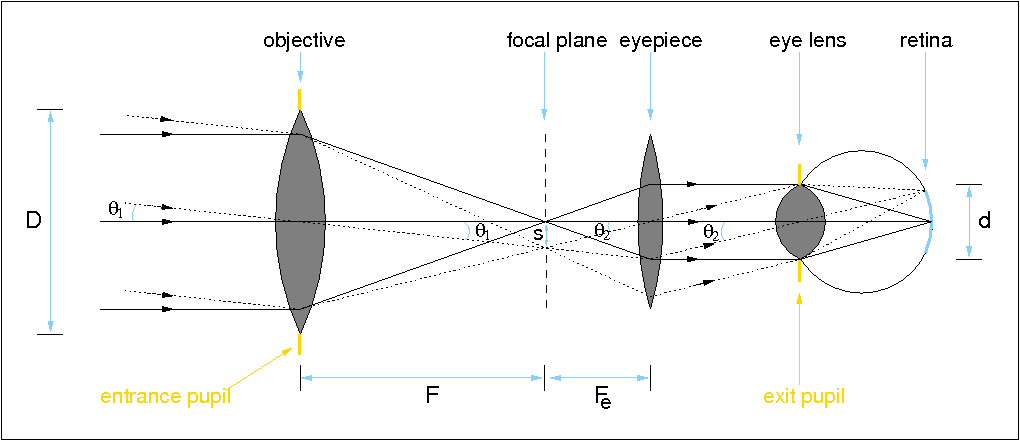
The role of the eyepiece can be thought of as a magnifying glass which takes the diverging rays of light from each point in the focal plane and makes them parallel. The lens in the eye then focuses this parallel light, creating an image of the object on the retina which is the correct way up. However, since the brain inverts all images falling on the retina (if it didn't, the everyday world around us would look upside down!), the view in a telescope appears upside down. As can be seen from figure 27, the image recorded by an electronic detector placed at the focal plane of the objective would also appear upside down.

Looking in more detail at figure 27, it is useful to define the following terms: the entrance pupil is the area at the entrance of the telescope that can accept light. Clearly, in figure 27, this is defined by the objective lens. The exit pupil is the image of the entrance pupil formed by the eyepiece. Only rays which pass through the exit pupil can exit the system, and it therefore represents the optimum position for the eye when observing with a telescope. If the eye is placed closer or further away from the eyepiece than the exit pupil, not all the light gathered by the telescope will be collected by the eye. Light is also lost if the diameter of the exit pupil is greater than the size of the dark-adapted pupil of the eye, i.e. about 8mm. The distance of the last lens of the eyepiece to the exit pupil is known as the eye relief, and for comfortable viewing is usually designed to be around 10mm in an amateur telescope.

For simplicity, figure 27 assumes that the eyepiece (or ocular) is a single positive lens. We have already seen that such a lens would introduce chromatic aberration and hence combinations of lenses are often used. The simplest combinations, composed of two lenses, are the Huygens and Ramsden eyepieces. More complex, and expensive, eyepieces use three or more lenses and are able to provide better correction for chromatic aberration, wider aberration-free fields-of-view, and comfortable eye relief. Common designs are the Kellner, Orthoscopic, Plössl, Erfle and Nagler eyepieces, some of which are shown in figure 28.

figure 28:

Photograph of some typical telescope eyepieces. There is a huge variety of designs, with very different sizes and weights, and prices ranging from tens of pounds to many hundreds.

Magnifying power

From figure 27, it can be seen that the objective, of focal length F, focuses parallel light to a point image in its focal plane; the eyepiece, of focal length F_e, takes a point source in its focal plane and converts it back to parallel light. Two distant point sources separated by an angle ₁ will produce two point images separated by a distance s = F ₁ in the focal plane of the objective and, since this is also the focal plane of the eyepiece, the resulting two beams of parallel light will diverge at an angle ₂ = s / F_e. Hence, an observer looking through the eyepiece will see parallel light from two sources separated by an angle ₂ on the sky. Without the help of the telescope, the eye would receive parallel light from the two sources separated by an angle ₁. Therefore, since ₂ > ₁, the image has been magnified. Given that s = F ₁ = F_{e 2}, the magnification (or magnifying power) of the telescope/eyepiece combination is simply defined as:

M = ₂ / ₁ = F / F_e.

When the magnification of a telescope is defined in this manner, it clearly only has any meaning when the telescope is being used with an eyepiece. Hence magnification is not a term used in the research vocabulary of professional astronomers, whose telescopes are never used visually. The term is relevant to the amateur astronomy market, of course, but it is often misused as the primary indicator of telescope performance. As we have seen, it is the diameter, focal length and telescope design which affect the performance of a telescope; the magnification is something which can be altered simply by using different eyepieces and is not an inherent property of the telescope.

Magnification limits

A further inspection of the on-axis rays in figure 27 shows that the triangle formed by the diameter of the objective, D, and the image in the focal plane at a distance F from the objective is similar to the triangle formed by the diameter of the exit pupil at the eyepiece, d, and the image in the focal plane at a distance F_e from the eyepiece, i.e.

D / d = F / F_e = M.

Hence an alternative way to express magnification is as the ratio of the diameters of the objective and the exit pupil. This naturally leads to a lower limit to the useful magnification of a telescope; the magnification must be sufficiently high to make the exit pupil equal to or smaller than the diameter of the dark-adapted pupil of the eye, otherwise not all of the light collected by the telescope will be gathered by the eye. This condition can be written as

M ≥ D / d,

where d is now the diameter of the eye's pupil.

Another lower limit to the useful magnification of a telescope can be obtained by comparing the resolving power of the telescope to that of the eye. It is impossible to separate two point sources by increasing the magnification if they are not resolved in the focal plane. However, if the two point sources are resolved in the focal plane, it is possible to use magnification to bring them above the resolution limit of the human eye. Hence a lower limit to the useful magnification of a telescope is the factor by which its resolution, , needs to be multiplied by to make it equal to the resolution of the eye, _e; any lower, and the full resolving power of the telescope is not being properly exploited. This limit can be expressed mathematically as

M ≥ _e / .

Assuming that the resolution of the telescope is limited by diffraction, and that the resolution of the eye is approximately four times its diffraction limit (due to the relatively poor quality of the eye lens), this equation can be rewritten as

M ≥ 4 x (1.22 / d) / (1.22 / D) = 4 D / d.

Assuming again that the diameter of the dark-adapted eye pupil, d, is 8mm, we finally obtain

M ≥ D / 2,

where D is expressed in mm. Hence, matching the resolution of the telescope to the resolution of the eye imposes a lower magnification limit which is four times higher than that imposed by the exit pupil diameter.

It is not possible to increase the magnification of a telescope indefinitely by changing the eyepiece. Ultimately, magnification is limited by the difficulty in making usable eyepieces of very short focal length and by the progressive impairment of vision as the beam that the eye accepts becomes smaller than about 1mm. Hence, using the expression derived above for the magnification of a telescope in terms of the diameters of the objective and exit pupil, we get

M ≤ D,

where D is again expressed in mm. Hence an 8-inch (200mm) reflector will have a useful upper magnification limit of approximately 200.

An example problem shows how these magnification limits can be used in practice. It should be emphasized, however, that the magnification limits described here are only guides, and the actual limits of magnification depend on numerous factors, such as the characteristics of the astronomer's eye and telescope, the atmospheric conditions and the objects being observed.

Visual resolving power

The theoretical resolving power, , of a telescope based on Rayleigh's criterion can be written as

≈ 140 / D,

where is in arcseconds, D is in mm, and we have assumed an observing wavelength of 550nm.

A skilled observer, however, can actually resolve two stars which are separated by an even smaller angle than given by this expression. This is possible because an acute eye in good observing conditions can actually detect a drop in the intensity between two close point sources of only 5%, whereas the drop in intensity implied by Rayleigh's criterion is 20%. A number of alternatives to Rayleigh's theoretical criterion have therefore been proposed, including Dawes empirical criterion, which can be approximated by:

≈ 115 / D,

where is in arcseconds, D is in mm and we have again assumed an observing wavelength of 550nm. Hence Dawes' limit gives resolving powers which are about 20% better than Rayleigh's limit. Sparrow's limit is even smaller, stating that it is possible to resolve objects even when they are separated by half of the angle given by Rayleigh's criterion, although to do this requires the use of electronic detectors and data analysis techniques to search for the flat-topped intensity profile of the two closely-separated point sources.