| fluxes and magnitudes |
|
The brightness of an astronomical source is usually given either in relative terms - the magnitude scale, or in absolute terms - the flux scale. The former is a logarithmic brightness scale, whereas the latter is a linear brightness scale. You will have already come across fluxes and magnitudes during the first-year astronomy course at Sheffield, but it is useful to revisit the basic concepts here.
fluxes
Before defining flux, it is important to define luminosity. The luminosity, L, of a source is defined as the total amount of radiant energy emitted over all wavelengths per unit time in all directions. The units of luminosity are joules per second (J s-1) or watts (W), so you can think of luminosity as the power of the source.
Of course, it is impossible to intercept all of the energy
emanating from an astronomical source and measure it. In practice,
only a small fraction of the energy is ever detected, the fraction
depending on the area of the collector and the distance of the
collector from the source. This collected quantity is known as the
flux, F, and has units of watts per square metre (W
m-2). The fraction of the luminosity collected by every
square metre of detector located a distance d m from the
source is simply the luminosity divided by the surface area of a
sphere of radius d which is centred on the source, i.e.
F = L / 4 ![]() d2,
d2,
which shows that the flux obeys an inverse-square law with distance.
The electromagnetic radiation from most astronomical sources spans
many orders of magnitude of wavelength and it is not possible to
measure the flux at all wavelengths using the same equipment. Hence
the flux is often measured within a limited wavelength range and
quoted in terms of unit wavelength interval,
Fλ (in units of W m-2
nm-1), or unit frequency interval, F![]() (in units of W m-2
Hz-1). Both Fλ and
F
(in units of W m-2
Hz-1). Both Fλ and
F![]() are usually referred to
as the monochromatic flux (or flux density) and, as
the monochromatic fluxes of astronomical sources are small, the
jansky (Jy) unit is often used, where 1 Jy = 10-26
W m-2 Hz-1. F
are usually referred to
as the monochromatic flux (or flux density) and, as
the monochromatic fluxes of astronomical sources are small, the
jansky (Jy) unit is often used, where 1 Jy = 10-26
W m-2 Hz-1. F![]() and Fλ are related by
the equation:
and Fλ are related by
the equation:
F = Fbol = 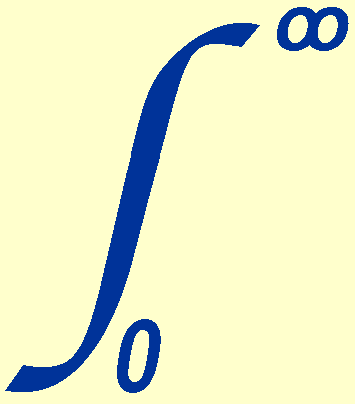 F
F![]() d
d![]() =
=
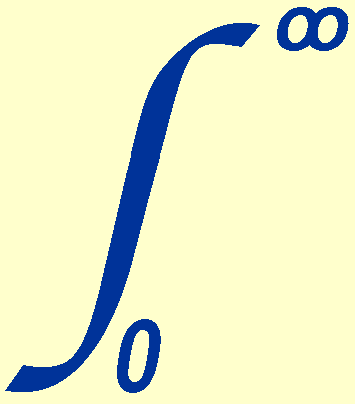 Fλ dλ.
Fλ dλ.
The flux, F, in the above equation is also sometimes referred
to as the bolometric flux, Fbol (also in units of W
m-2), as it represents the total flux emitted over all
wavelengths or frequencies.
Conversion between Fλ and
F![]() can be achieved using
the relations F
can be achieved using
the relations F![]() d
d![]() = Fλ
dλ (which follows from differentiating the above
integral) and c =
= Fλ
dλ (which follows from differentiating the above
integral) and c = ![]() λ, leading to
λ, leading to
F![]() = Fλ
λ2 / c, and
= Fλ
λ2 / c, and
Fλ = F![]() c /
λ2.
c /
λ2.
You need to be careful with units when using the above flux conversion
equations. For example, when converting
from Fλ in units of W m-2 nm-1 into F![]() in units of W m-2 Hz-1, you
need to enter λ in units of nm and c in units of
nm/s. Alternatively, you can convert Fλ to units of
W m-2 m-1 by multiplying by 109 and
then enter λ and c in units of m and m/s,
respectively.
in units of W m-2 Hz-1, you
need to enter λ in units of nm and c in units of
nm/s. Alternatively, you can convert Fλ to units of
W m-2 m-1 by multiplying by 109 and
then enter λ and c in units of m and m/s,
respectively.
Conversion of Fλ or F![]() to the photon flux,
Nλ or N
to the photon flux,
Nλ or N![]() , can be achieved using the relation E =
h
, can be achieved using the relation E =
h![]() = hc /
λ, leading to
= hc /
λ, leading to
N![]() = F
= F![]() / E = F
/ E = F![]() λ /
h c, in units of photons s-1 m-2
Hz-1, and
λ /
h c, in units of photons s-1 m-2
Hz-1, and
Nλ = Fλ / E =
Fλ λ / h c, in units of photons
s-1 m-2 nm-1.
magnitudes: definition
The Greek astronomer Hipparchos is usually credited with the origin of the magnitude scale. He assigned the brightest stars he could see with his eye a magnitude of 1 and the faintest a magnitude of 6. However, in terms of the amount of energy received, a sixth magnitude star is not 6 times fainter than a first magnitude star, but more like 100 times fainter, due to the eye's non-linear response to light. This led the English astronomer Norman Pogson to formalize the magnitude system in 1856. He proposed that a sixth magnitude star should be precisely 100 times fainter than a first magnitude star, so that each magnitude corresponds to a change in brightness of 1001/5 = 2.512. For example, a star of magnitude 2 is 2.5121=2.512 times fainter than a star of magnitude 1, a star of magnitude 6 is 2.5122=6.3 times fainter than a star of magnitude 4, and a star of magnitude 25 is 2.5125=100 times fainter than a star of magnitude 20. Note how it is only the magnitude difference that determines the brightness ratio of two stars, not the absolute values of their magnitudes.
Hence, Pogson's ratio of 2.512 leads us to Pogson's
equation:
F1/F2 =
2.512-(m1-m2),
where F1 and F2 are the fluxes
of two stars, m1 and m2 are
their magnitudes, and the minus sign in front of the exponent accounts
for the fact that numerically larger magnitudes refer to fainter
stars. It is important to note that the flux, F, in the above
equation, and all the equations given below, refers to any
linear measurement of the brightness of a star, e.g. the
number of counts, joules, photons, etc, received.
Taking logarithms of Pogson's equation, we obtain:
log10(F1/F2) = -(m1-m2) . log10(2.512) = -0.4 (m1-m2).
More conveniently, we can write:
F1/F2 =
10-0.4(m1-m2), and
m1-m2 = -2.5 log10(F1/F2).
Note that the factor of 2.5 in the latter equation is not equal to
2.512 rounded down. It is an exact value, due to the fact that
log10(2.512) = log10(1001/5) = 0.2
log10(100) = 0.2 x 2 = 0.4 = 1/2.5, precisely.
magnitudes: apparent and absolute
The magnitude of a source, m, defined above is known as
the apparent magnitude, as it is the value measured from the
Earth and does not take into account the distance of the source: a
star may be intrinsically brighter than another star and yet have a
higher apparent magnitude because it is further away from the
Earth. To represent the intrinsic brightness of a star, the
absolute magnitude, M, is used, which is defined as
the apparent magnitude a star would have if it is 10 parsecs (pc) from the
Earth, in the absence of any interstellar extinction. Hence, due
to the fact that the flux of a source drops as the inverse square
of the distance, d, we can write
Fd/F10pc =
[L / 4 ![]() d2] /
[L / 4
d2] /
[L / 4 ![]() 102] =
1/(d/10)2,
102] =
1/(d/10)2,
and
md-m10pc = -2.5 log10(Fd/F10pc).
Hence,
log10(Fd/F10pc) = log10(1) - 2 log10(d/10),
and we can then write:
md-m10pc = -2.5 [0 - 2 log10(d/10)],
or,
m - M = 5 log10(d/10).
This equation relates the apparent and absolute magnitude of a source
with its distance, where d is in parsecs. For example, the
brightest star in the sky, Sirius, has an apparent magnitude of
m = -1.5 and distance of d = 2.6 pc, so it has an
absolute magnitude of M = 1.4. The quantity m - M is
known as the distance modulus. If m - M = 0, 5, 10,
15, 20, 25 magnitudes, then d = 10 pc, 100 pc, 1 kpc, 10 kpc,
100 kpc and 1 Mpc, where 1 pc = 3.26 light years.
magnitudes: zero points
It can be seen that the magnitude scale is a relative one that depends on the ratio of the fluxes of two stars. It makes sense, therefore, to define a zero point, i.e. to choose a star that represents a magnitude of 0. We can then measure the magnitudes of all other stars with respect to this one. The A0V star Vega was chosen as this so-called primary standard because it indeed does have a magnitude close to zero as determined by Hipparchos' crude system, it is easily observable in the northern hemisphere for more than 6 months of the year, it is non-variable, relatively nearby (and hence unreddened by interstellar dust), and it has a reasonably flat and smooth optical spectrum. However, because Vega is too bright to observe with modern telescopes and instruments without saturating their detectors, and because it is not always observable, an all-sky network of fainter secondary standards has also been defined, where the magnitude of each star relative to Vega has been carefully calibrated. Over the years, refinements in the definition, number and measurement accuracy of the primary and secondary standards has resulted in the apparent magnitude of Vega now being 0.03 in the V-band, and it is also thought that Vega may be slightly variable, but for the purposes of this course we can ignore this few per cent offset and assume it is 0 in all bands.
If we have measured the flux of a standard star,
Fstd, and we know its catalogue magnitude,
mstd, we can determine the magnitude of another
star, m1, whose flux, F1, we
have also measured, as follows:
m1-mstd = -2.5 log10(F1/Fstd).
Rearranging this equation, we obtain:
m1 = mstd - 2.5
(log10F1 - log10Fstd) =
mstd + 2.5 log10Fstd - 2.5
log10F1.
The first two terms on the right-hand side of the above equation can
be collected together into what is known as the zero point,
mzp = mstd + 2.5
log10Fstd , giving
m1 = mzp - 2.5
log10F1.
A useful way of thinking about zero points is to note that the above
equation can be rewritten as:
m1 - mzp = - 2.5 log10
(F1/1).
This means that if F1 is the number of counts,
photons or joules received per second from a star of magnitude
m1, then the zero point is the magnitude of a star
that would give one count, photon or joule per second when
measured with the same equipment.
magnitudes: rule of thumb
A useful rule of thumb when thinking about magnitudes is that:
| -26.7 | = | Apparent V-band magnitude of the Sun
| -12.9 | = | Apparent V-band magnitude of the Full Moon
| -4.7 | = | Apparent V-band magnitude of Venus (brightest planet) | -1.5 | = | Apparent V-band magnitude of Sirius (brightest star) | 0 | ~ | Apparent V-band magnitude of Vega ( | 6 | ~ | Apparent V-band magnitude of the faintest stars visible to the naked eye under good conditions | 16 | ~ | Apparent V-band magnitude of the faintest stars visible to the eye through a 16'' telescope | 30 | ~ | Apparent V-band magnitude of the faintest objects detected by the Hubble Space Telescope
| |